编者按：随着近年来深度强化学习技术的发展，学术界提出了一些利用深度强化学习解决订单执行问题的方法。微软亚洲研究院与上海交通大学合作在 AI+ 金融领域的最新研究工作《Universal Trading for Order Execution with Oracle Policy Distillation》就是利用了强化学习技术，来尝试优化金融市场交易中订单执行（Order Execution）的问题。该工作已被 AAAI 2021 接收。

深度强化学习（Deep Reinforcement Learning）是近年来人工智能领域备受关注的技术和方向之一，已在多个领域取得了显著的研究成果。如今，学术界和产业界纷纷开始尝试将深度强化学习应用于现实世界。在 AAAI 2021 被接收的论文中，微软亚洲研究院与上海交通大学合作在 AI+ 金融领域的最新研究工作《Universal Trading for Order Execution with Oracle Policy Distillation》就是尝试利用强化学习，来优化金融市场交易中订单执行（Order Execution）的问题。该工作在训练过程中引入了能利用未来信息的先知策略（Oracle Policy），通过策略蒸馏的方式，指导只能看到当前信息且在实际场景中最终使用的策略学到更优的交易策略。

得益于微软亚洲研究院于2020年9月开源的 AI 量化投资平台 Qlib，研究员们在进行《Universal Trading for Order Execution with Oracle Policy Distillation》研究工作的尝试和迭代的同时，还积极构建了能更好地支持算法交易场景下强化学习研究的组件，使得研究思路得以在这个组件上快速方便地进行尝试和迭代，并为今后的研究课题打下了基础。该研究工作的部分相关代码目前已通过样例的形式在 Qlib 中开源，后续研究员们会将完整的支撑组件嵌入到 Qlib 中，旨在助力算法交易场景下各类问题的研究。

什么是订单执行

以最大化长期收益为目标的投资行为往往涉及一系列针对资产组合（Portfolio）的调整，这中间就包括订单执行任务。以股****投资为例，如图1所示，若投资人想要进行股****持仓的调整，则需要通过执行一系列买单或卖单来买入或卖出一定数量的特定股****。

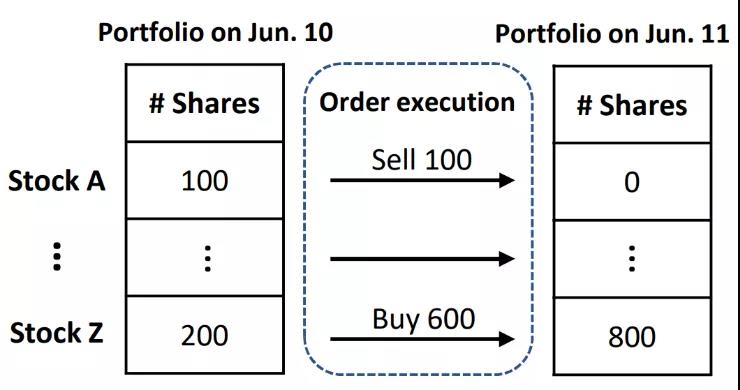
图1：投资组合的变更需要买单和卖单的执行

订单执行有两个主要目标：

1）在规定时间窗口内，完成对全部订单的交易；

2）同时最大化收益（或最小化成本）。

订单执行任务的形式化表述如图2所示。以卖单为例，卖单需要最大化不同时刻以 p_t 价格卖出数量为 q_t 的股****所得的现金，同时满足所有时刻的总卖出量为 Q。这里的 Q 一般是上层投资策略给出的换仓决策。

要做到这一点，其主要挑战是如何在减小市场价格影响（Price Impact）的同时降低价格风险（Price Risk）。所谓价格影响指的是在短时间内执行大量交易影响了市场价格，而造成价格向不利于交易的方向移动。一味地拖长交易时间会增大价格风险，即由于交易周期拉长而错过了价格最有利的交易时机。从这里可以看到，不同时刻之间的交易决策互相之间会有影响。所以订单执行问题，可以认为是一个序列决策（Sequential Decision Making）问题。

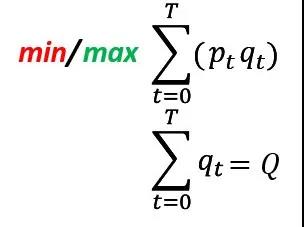
图2：订单执行问题的数学表述（卖单最大化收益，买单最小化成本）

传统的订单执行方法

传统的订单执行策略往往是基于模型（Model-based）的，这些方法需要对市场价格的变化做一些假设以建立近似的市场模型。例如 [1] 中假设价格的变化在随机游走的基础上与策略在此前执行的订单量线性相关。有了这些市场模型，就可以使用基于动态规划（Dynamic Programming）思想的随机控制（Stochastic Control）理论等相关方法求解最优的执行策略。但是这些假设相对于真实的市场往往太过简单，与真实的市场相去甚远，从而导致基于这些模型的策略在真实场景与数据的回测中表现不佳。

基于强化学习的订单执行

正如前文所说，订单执行本身是一个序列决策问题，并且有明确的优化目标，所以很符合强化学习的应用场景。随着近年来深度强化学习技术的发展，学术界提出了一些利用深度强化学习解决订单执行问题的方法。这些方法摆脱了传统方法中不切实际的价格波动假设，利用无模型算法直接优化执行策略，取得了优于传统方法的表现。

但是，这些方法都是对每只股****单独训练交易策略，这样不仅低效，而且由于数据量较小容易产生过拟合的问题。同时，强化学习的训练本身需要大量高质量的数据，而金融市场数据的信噪比极低，直接使用已有的无模型强化学习方法的采样效率很低，很难学习到合理的交易策略。

全股交易策略

为了提高训练效率，充分利用所有数据，研究员们设计了一个归一化的奖励函数，使得策略能够针对全股进行优化，而非专门针对单一股****进行决策优化。如图3所示，在奖励函数中，p ̃ 为给定股****在整个交易时间段内的平均价格，p_t 为 t 时刻的价格，Q 为订单总量，q_t 为 t 时刻的交易量。在 t 时刻，用总订单量归一化 t 时刻交易量，用平均价格归一化 t 时刻价格，从而可以用全股的数据优化强化学习策略。

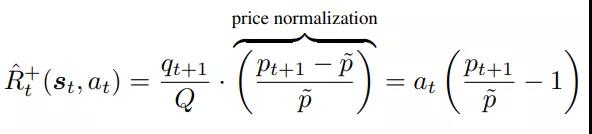
图3 ：归一化的奖励函数设计

先知策略蒸馏

在强化学习的训练中，智能体只能观察到不完美的市场信息（Imperfect Information），即历史上已经发生的事件和市场状态，但由于股****市场未来的变化难以预测，且金融数据信噪比较低，因此导致智能体很难学习到市场状态的合理表示，也无法学习到合理的交易策略。如图4所示，一种先知策略蒸馏 (Oracle Policy Distillation, OPD) 的方法被研究员们设计出来，以弥合不完美的市场信息和所希望的最优交易行为之间的鸿沟。

具体来说，将完美的信息作为输入训练一个先知策略（Oracle Policy），该策略容易学到最优的交易行为，然后再利用策略蒸馏（Policy Distillation）方法，让先知策略作为“教师”，指导只能观察到不完美信息的“学生”（普通策略）进行学习。在真实的交易场景下，则没有先知“教师”的参与，只有普通策略自行交易。

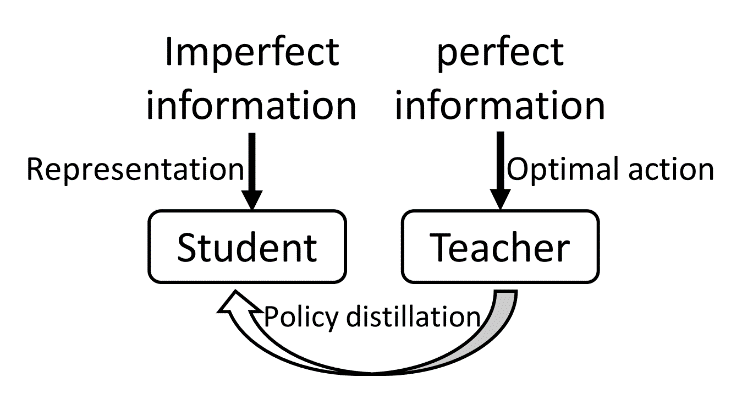
图4：基于教师-学生框架的先知策略蒸馏示意图

如图5所示，在订单执行的场景中，当智能体在时刻 t 做出决策时，不完美信息指的是在时刻 t 之前的市场信息，而完美信息则指的是在整个时间范围上，包括未来的市场信息（由于先知策略只在训练阶段发挥作用，所以可以获得这部分信息）。通过让先知看到完美信息，那么它可以比较容易地学习到最优的策略，从而作为“教师”指导“学生”策略。

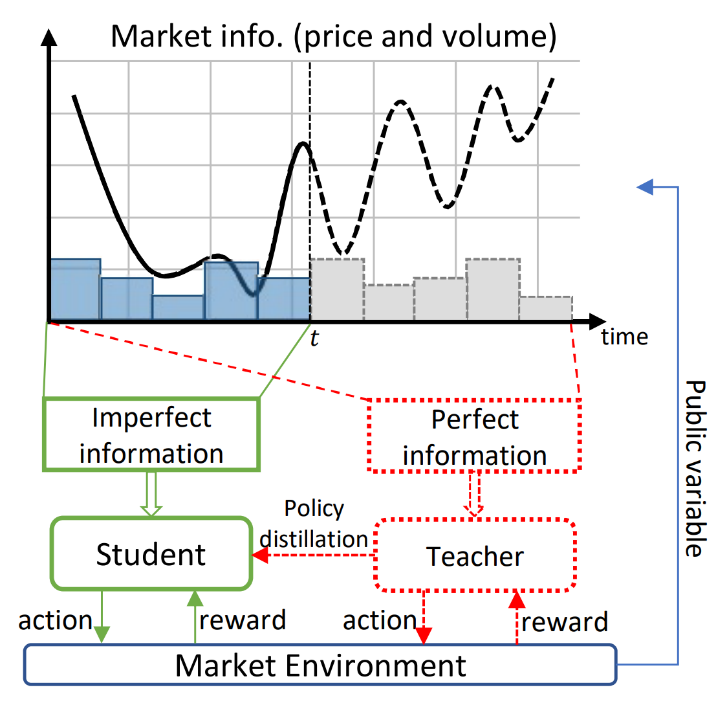
图5：教师-学生框架的流程示意图

为了让“学生”能从“教师”那里学习到最优的交易决策，研究员们在强化学习优化算法 PPO [2]（ Proximal Policy Optimization）的损失函数基础上，增加了图6的蒸馏损失（Distillation Loss），最小化“学生”和“教师”行为之间的负似然（Negative Log-likelihood）损失，从而使得“学生”的决策能和“教师”选择的最优策略更加接近。

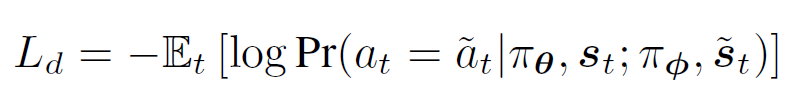
图6：先知策略蒸馏的损失函数

实验设置和订单执行结果

该研究基于微软 AI 量化投资开源平台“微矿 Qlib”进行了所有方法的训练和回测。实验在 A 股2017年1月到2019年6月的分钟级股****量价数据集上进行，并按照时间切分了训练、验证和测试集，如表1所示。

表1：训练集、验证集、测试集的切分

研究员们将该方法和基于模型的传统方法以及无模型的强化学习方法两类进行了比较，并比较了“有/无教师策略指引”的结果，表2为回测评估结果。研究工作的先知策略蒸馏方法（OPD）显著超越了其它已有方法，也超过了“无教师指引的学生”（OPD^S），取得了更高的奖励（Reward）和价格优势（Price Advantage, PA）。

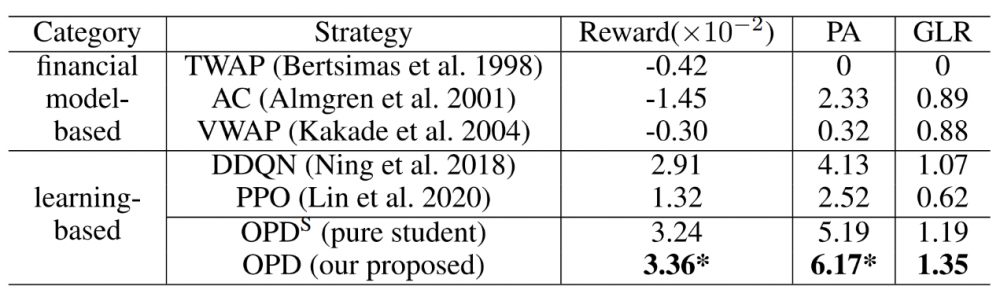
表2：回测评估结果 （* 代表显著性测试结果 p 值小于0.01）

如图7所示，从学习曲线中可以看出，OPD 和 OPD^S 在验证集上的效果差距相比训练集明显提升，这也表明了先知策略的指引可以让“学生”学习到泛化性更好、更有效的交易策略。

图7：在训练集与验证集上的学习曲线

执行结果分析

图8则展示了多个强化学习方法生成的策略的最终订单执行结果，其中 OPD^T 代表先知策略。可以看到，OPD 往往能做出和 OPD^T 一致或相似的行为（case 1,2），这表明先知策略蒸馏确实让“学生”学习到了合理的策略。然而，当不完美信息与完美信息差距过大时，例如在一天的开始阶段，由于可观察到的信息太少，所以 “学生”很难做出完美的决策，往往会错过一天开始阶段的最优交易机会（case 3）。但即便如此，“学生”也能在接下来的时间中做出次优的决策来弥补损失，其效果仍超越了其它的方法。

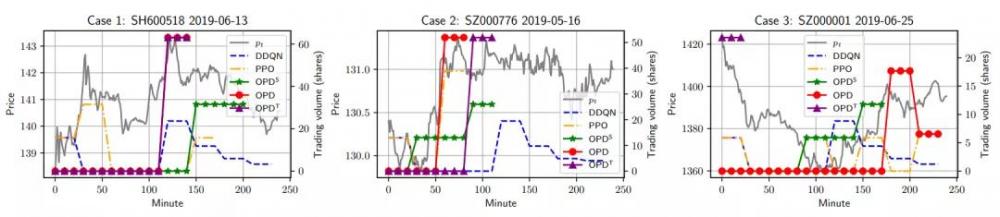
图8：不同策略执行订单的三个回测案例

强化学习订单执行组件

研究工作的订单执行实验基于 Qlib 框架构建，其设计思路如图9所示。这里采用了多环境并行执行的设计思路，并针对金融交易场景做了一系列适配与优化，极大提高了回测效率与算法优化的效率。不同环境执行的结果由采集器（Collector）统一收集并交给策略模块进行学习与优化。其中，策略模块既支持传统的 TWAP、VWAP、Almgren-Chriss 策略，也支持最新的深度强化学习策略。该框架的算法样例已经开源，完整框架与 Qlib 的集成目前正在积极开发中。

算法样例开源链接（点击阅读原文即可访问）：

https://github.com/microsoft/qlib/tree/high-freq-execution#high-frequency-execution 

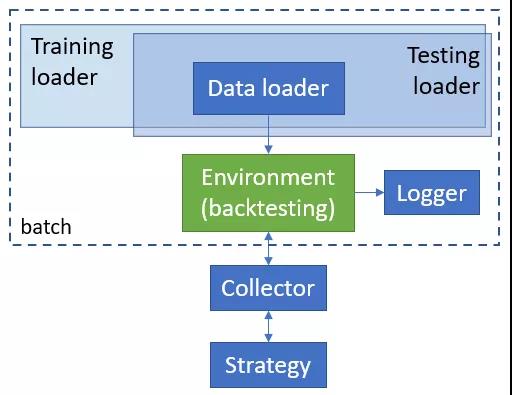
图9 ：强化学习交易优化组件设计图

参考资料：

[1] Bertsimas, D.; and Lo, A. W. 1998. Optimal control of execution costs. Journal of Financial Markets 1(1): 1–50.

[2] Schulman, John, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. "Proximal policy optimization algorithms." arXiv preprint arXiv:1707.06347 (2017).

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。